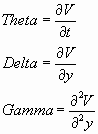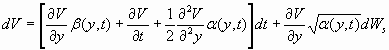
Black Scholes Differential Equation
Ito's formular enable us to approach the problem more general.
We assume again a derivative V(y(t),t) that depends on time t and an underlying asset y(t). The derivative is due at time T.
We get the differential equation below by applying Ito's formula to the derivative process V(x(t),t).
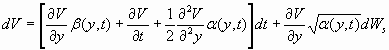
The next step leads us to the basic idea of hedge fonds. We construct a portfolio P(t) consisting of the asset x(t) and its derivative V(x(t),t) and combine both in such away that a risk less yield could be achieved.
![]()
We assume that y(t) obeys the geometrical Wiener process with a risk less interest rate b .
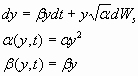
Now we combine the geometrical Wiener process and the portfolio P(t):

The diffusion term disappears when the following relationship is satisfied. This relationship is called also hedge ratio forming the core idea of hedge fonds.
![]()
A risk less portfolio remains since the diffusion term disappears. R denotes the risk less yield defined for the portfolio P(t):
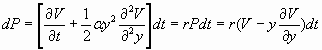
We get the Black Scholes differential equation by some rearrangements of the equation above.
![]()
The Greek's which are usually available for derivatives are defined as following: